How 3D Models are Stored in .dwg part2

Using Boolean Operations to Create 3D Models

In the previous article, I talked about the differences by which 3D models are stored in CAD files, as compared to how they are constructed by designers. Designers do not need to describe the shapes of the models they’re designing with mathematical formulae. Instead, the application's user interface transparently makes calls to the modeler’s functions, in accordance with the algorithms created by CAD developers.

One of the Open Design Alliance APIs (short for “application programming interface”) that undertakes 3D modeling is the OdDb3dSolid interface. The modeling methods provided by the interface can be divided into two groups. One group involves operations on bodies as they are: creation bodies and Boolean operations on them. The other group includes modification of solids based on topological elements.

Boolean Operations

Using Boolean operations on bodies is a powerful tool as it is visual, intuitive, and applicable to many modeling tasks. At the same time, the corresponding section of the ODA platform's API is most concise, with only one method:

OdResult OdDb3dSolid::booleanOper(OdDb::BoolOperType operation, OdDb3dSolid* solid);

The first argument defines the type of the operation: Unite, Intersect, or Subtract.

namespace OdDb
{
  enum BoolOperType
  {
    kBoolUnite     = 0,
    kBoolIntersect = 1,
    kBoolSubtract  = 2
  };
}

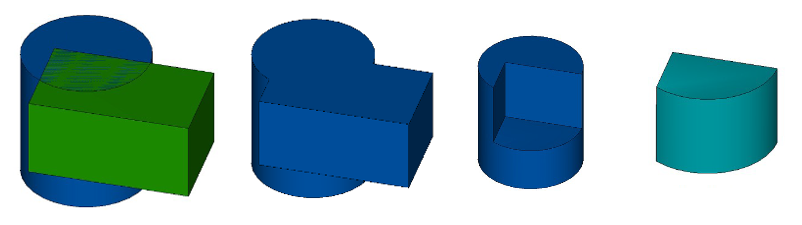
If the problem of what can be arguments for Boolean operations is somehow solved, then the tree of Boolean operations is sufficient to describe entire body shapes. This principle underlies a large section of modeling called Constructive Solid Geometry (or “CSG” for short). The essence of this approach is that the leaves of the construction graph are elementary bodies, such as parallelepipeds, cylinders, and spheres.

Defining Elementary Bodies

ODA API provides a comprehensive set of methods for creating elementary bodies, such as these:

void createBox( double xLen, double yLen, double zLen );
void createFrustum( double height, double xRadius, double yRadius, double topXRadius );
void createSphere( double radius );
void createWedge( double xLen, double yLen, double zLen );
void createTorus( double majorRadius, double minorRadius );

All elementary bodies are created in the global coordinate system. Parallel movement, rotation around axes, and scaling are used to position bodies in space. Operational parameters are presented as a matrix in the form of a 3-by-3 square rotation matrix. This is effectively expanded to a 4-by-4 matrix by an additional column and row that store the offset vector and the scaling coefficients along the coordinate axes.

locMatr = OdGeMatrix3d::rotation( OdaPI2, OdGeVector3d::kXAxis ) * OdGeMatrix3d::translation( OdGeVector3d::kXAxis * 100.0 );
///...
pSolid->transformBy(locMatr);

Broadly defined, the CSG approach is sometimes considered to be the modeling of solids using Boolean operations over a class of bodies which is wider than the class of elementary bodies.

Sweeping Bodies

As a rule, swept bodies are included in the list of the operations' operands. A swept body is constructed using two curves: the sweep contour and the sweeping path. When it comes to the sweeping path, of particular importance is the straight line and the circular arc, as well as the extrusion and revolution bodies that correspond to them. ODA API provides the following functions to create sweeping bodies:

OdResult extrude(const OdDbRegion* region,  double height,  double taper,  bool isSolid = true);
OdResult revolve(const OdDbRegion*   pRegion,  const OdGePoint3d&  axisPoint, const OdGeVector3d& axisDir,  double angleOfRevolution);
OdResult extrudeAlongPath(const OdDbRegion* region, const OdDbCurve*  path, double   taperAngle = 0.0, bool isSolid = true);

I'd like to draw your attention to an interesting feature of API: it has a cone parameter that is responsible for the smooth scaling of the swept contour along the extrusion path.

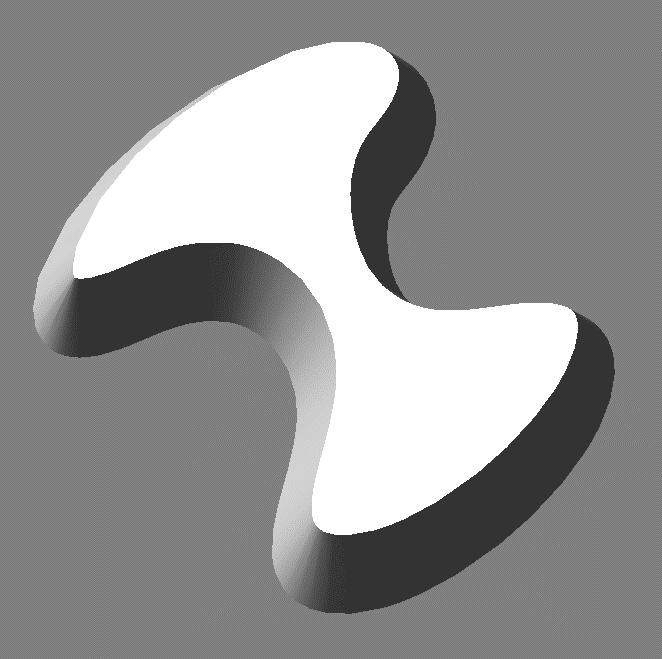
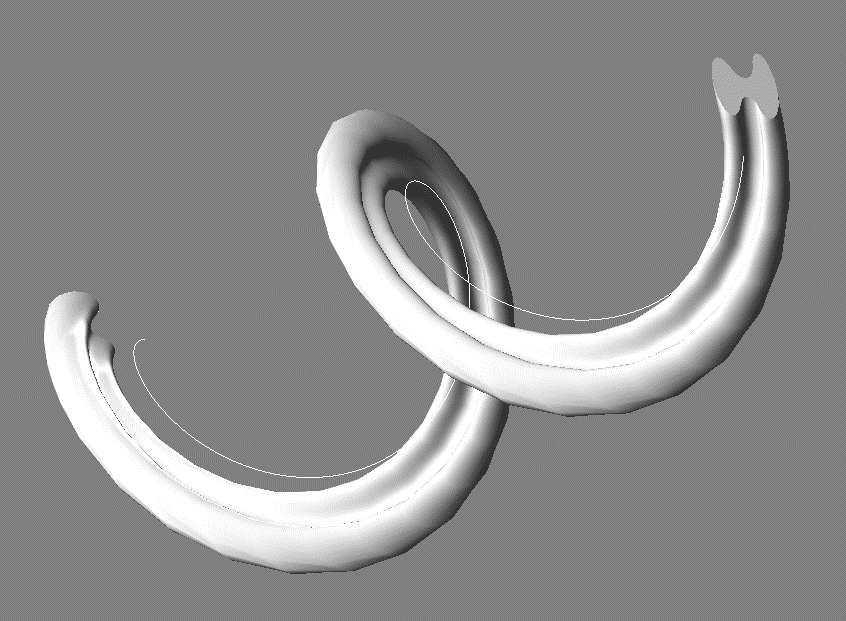
There are other ways to create bodies but, without mentioning them, in my view the power of the extended CSG is clear. It's an impressive tool for creating bodies with complex shapes. Moreover, the formalized constructive geometry can become the basis for storing models in the form in which they were created by designers.

It might seem that constructive representation has very serious advantages over the boundary one. The way, how to generate topological elements during the design process isn’t clear unlike direct construction from simple enough primitives. But the fact is that for description of bodies’ shape boundary representation was selected. In this regard, an important aspect of 3D modeling must be mentioned: the possibility of controlled modification of the body shape.

In my next article, I'll discuss the problem of local modifications of solid bodies.